GUIA DE MATEMATICAS PARA GRADO NOVENO GUILLERMO RIOS CAÑAS Enlace para las clases: https://meet.google.com/igv-cghd-aef

• Santiago de Cali, Febrero 6 del 2021

DOCENTE: GUILLERMO RIOS CAÑAS

CONTACTO:  WHATSAAP 3187948188

PLAN DE  AREA DE MATEMATICAS:   ENLACE:

https://drive.google.com/folderview?id=1ZQojFaqS9iLRK3ixXsNkTADbESVk0bpS

GUIA ORIENTADORA DE ALGEBRA PARA EL PRIMER PERIODO

LA GUIA SE DEBE COPIAR Y DESARROLLAR EN EL RESPECTIVO CUADERNO.

ESTANDAR: Construyo expresiones algebraicas equivalentes a una expresión algebraica dada.

DESEMPEÑOS, DBA Y CLG.

Expresa y traduce entre lenguaje verbal y simbólico.
* Evalúa expresiones algebraicas.
* Reconoce reglas de formación de términos de una sucesión.
* Construye tablas a partir de expresiones algebraicas.
* Reconoce que las letras pueden representar números y cantidades, y que se pueden operar con ellas y sobre ellas.
* Opera con formas simbólicas que representan cantidades.
* Reconoce procesos necesarios en la resolución de ecuaciones.
* Resuelve ecuaciones usando los procesos adecuados.
* Utiliza propiedades para determinar si un problema, que se representa a través de una ecuación, tiene o no solución.

APRENDIZAJES:

Reconoce el lenguaje algebraico como forma de representar procesos inductivos.
* Utiliza propiedades y relaciones de los números reales para resolver problemas.

EJES CONCEPTUALES:

Notación algebraica (traducción de lenguaje natural a lenguaje algebraico)
* Sucesiones numéricas y geométricas (regla de formación en forma verbal, simbólica y numérica. Elaboración de tablas).

TRANSVERSALIDAD DE CATEDRAS:

Artística: Teselaciones
* Reconoce el patrón geométrico y los movimientos en el plano (rotación, traslación, simetría, reflexión, etc.) que generan la teselación.
* A partir de un patrón construyo una teselación, la coloreo y la expongo a mis compañeros.
Física: Ecuaciones importantes en física
Ejemplos: Ecuación de la velocidad, ecuación de la aceleración, ecuación de la fuerza, ecuación del movimiento parabólico, ecuación de la energía, etc.

ESTRATEGIAS DE EVALUACION:

Diseñar, implementar y evaluar
actividades que involucren situaciones
problemas que favorezcan la estructura
de solución análisis, operación y
respuesta. En la operación se debe tratar
de favorecer el cálculo de operaciones
aritméticas con números reales y
operaciones con expresiones algebraicas
y trascedentes. Y en la solución se debe
favorecer el análisis de la validez
* Exámenes cortos usando preguntas
pruebas saber 11 (base de datos ICFES).
* Exámenes cortos sobre problemas que
se resuelven usando modelos geométricos.
* Revisión de tareas y actividades
desarrolladas en clase por los estudiantes en el cuaderno.
* Reflexión y discusión en clase sobre el
plan lector, Participación y trabajo en
Clase.
* Autoevaluación. * Cumplimiento acuerdos de disciplina.
* Métodos de evaluación alternativos
que se ajusten a cada salón (trabajos
escritos, estudios estadísticos.

LA HISTORIA DEL ALGEBRA

La historia del álgebra comenzó en el antiguo Egipto y Babilonia, donde fueron capaces de resolver ecuaciones lineales (ax = b) y cuadráticas (ax² + bx +c = 0) entre otras. Los antiguos babilonios resolvían cualquier ecuación cuadrática empleando esencialmente los mismos métodos que hoy se enseñan.

Los matemáticos alejandrinos Herón y Diofante continuaron con la tradición de Egipto y Babilonia, aunque el libro “Las aritméticas” de Diofante es de mucho más nivel. Esta antigua sabiduría sobre resolución de ecuaciones encontró, a su vez, acogida en el mundo islámico, en donde se le llamó ciencia de reducción y equilibrio. La palabra árabe “al−jabru” que significa “reducción”, es el origen de la palabra álgebra. En el siglo IX, el matemático _Al−Jwrizm; escribió uno de los primeros libros árabes de álgebra, una presentación sistemática de la teoría fundamental de ecuaciones, con ejemplos y demostraciones incluidas. A finales del siglo IX, el matemático egipcio Abu Kamil enunció y demostró las leyes fundamentales e identidades del álgebra y resolvió problemas matemáticos muy complicados.

El álgebra en la antigua babilonia:

La principal fuente de información sobre la civilización y la matemática babilónica procede de textos grabados con inscripciones cuneiformes en tablillas de arcilla. Los textos se escribían sobre las tablillas cuando la arcilla estaba aún fresca. Después podían borrarse y usarse otra vez o también cocerse en hornos o simplemente se endurecían al sol. Las tablillas más antiguas que se conservan son del 2000 a.C. Varios miles de tablillas esperan todavía ser descifradas.

Estas tablillas han proporcionado abundante información sobre el sistema numérico y los métodos de cálculo que usaban. También las hay con textos que contienen problemas algebraicos y geométricos. Los babilonios disponían de fórmulas para resolver ecuaciones cuadráticas. No conocían los números negativos por lo que no se tenían en cuenta las raíces negativas de las ecuaciones. Su sistema de numeración era de base 60 y ha llegado hasta nosotros en la medida del tiempo y de los ángulos. Llegaron a resolver problemas concretos que conducían a sistemas de cinco ecuaciones con cinco incógnitas e incluso se conoce un problema astronómico que conduce a un sistema de diez ecuaciones con diez incógnitas. Tampoco conocían el cero lo que lleva a problemas de interpretación de las cantidades. A partir del siglo VI a.C., fue utilizado un signo de omisión, es decir una especie de cero.

El álgebra en la civilización egipcia:

Dejaron pocas evidencias matemáticas. El papiro es un material que resiste mal el paso del tiempo. Hay dos papiros de gran importancia: el papiro Rhind y el Moscú. El Rhind fue confeccionado hacia 1650 a.C. por un escriba llamado Ahmes quien dice haberlo copiado de un original doscientos años más antiguo. Expone 87 problemas y sus soluciones. El Moscú es parecido con 25 problemas y sus soluciones. En lo referente al álgebra, los papiros contienen soluciones a problemas con una incógnita.

El álgebra en la civilización china:

De la época de la primera dinastía Han (206 a. C. hasta 24 d.C.) procede el tratado

“Matemáticas en nueve Libros”. Posteriormente matemáticos como Liu Hui (siglo III), Sun-zi (siglos II-IV), Liu Zhuo (siglo VI) y otros hicieron aportaciones a este tratado. El texto trata problemas económicos y administrativos como medición de campos, construcción de canales, cálculo de impuestos etc. Tenían un procedimiento algorítmico para resolver sistemas de ecuaciones lineales parecido al que hoy conocemos como método de Gauss que les llevó al reconocimiento de los números negativos. Estos números constituyen uno de los principales descubrimientos de la matemática china.

La escuela algebraica china alcanza su apogeo en el siglo XIII con los trabajos de  Quin Jiushao, Li Ye, Yang Hui y Zhu Shi-jie que idearon un procedimiento para la resolución de ecuaciones de grado superior llamado método del elemento celeste o tian-yuanshu. Este método actualmente se conoce como método de Horner, matemático que vivió medio milenio más tarde.

El desarrollo del álgebra en esta época es grandioso: sistemas de ecuaciones no lineales, sumas de sucesiones finitas, utilización del cero, triángulo de Tartaglia (o Pascal) y coeficientes binomiales así como métodos de interpolación que desarrollaron  en unión de una potente astronomía.

Él álgebra en la civilización india:

Son muy escasos los documentos de tipo matemático que han llegado a nuestras manos, pese a tener constancia del alto nivel cultural de esta civilización. Aún más que en el caso de China, existe una tremenda falta de continuidad en la tradición matemática hindú y al igual que ocurría con las tres civilizaciones anteriores, no existe ningún tipo de formalismo teórico.

Los primeros indicios matemáticos se calculan hacia los siglos VIII-VII a.C, centrándose en aplicaciones geométricas para la construcción de edificios religiosos y también parece evidente que desde tiempos remotos utilizaron un sistema de numeración posicional y decimal. Fue, sin embargo, entre los siglos V-XII d.C cuando la contribución a la evolución de las matemáticas se hizo especialmente interesante, destacando cuatro nombres propios: Aryabhata (s.VI), Brahmagupta (s.VI), Mahavira (s. IX) y Bhaskara Akaria (s.XII). La característica principal del desarrollo matemático en esta cultura, es el predominio de las reglas aritméticas de cálculo, destacando la correcta utilización de los números negativos y la introducción del cero, llegando incluso a aceptar como números validos las números irracionales. Profundizaron en la obtención de reglas de resolución de ecuaciones lineales y cuadráticas. Matemáticamente se considera indiscutible la procedencia hindú del sistema de numeración decimal y las reglas de cálculo.

El álgebra en la civilización griega:

La Escuela Pitagórica (fundada en el siglo V a.C.) incorpora resultados de la tradición babilónica aritmética algebraica. La primera finalidad de esta secta era religiosa pero secundariamente, el desarrollo matemático que de ella se derivó fue enorme.

Destacamos la época del Álgebra Geométrica (450 – 300 a.C.), que trata los problemas algebraicos con la ayuda de construcciones geométricas. El núcleo lo constituye el método de anexión de áreas cuya finalidad básica era resolver ecuaciones. Este método se puede usar para resolver ecuaciones lineales y no lineales. En el tratado “Los Elementos” de Euclides se tratan diversas ecuaciones cuadráticas según los métodos del álgebra geométrica. También Teodoro de Cirene, Teeteto y Eudoxo de Cnido, consolidan este álgebra geométrica.

ACTIVIDAD No. 1

RESPONDER LAS SIGUIENTES PREGUNTAS DE ACUERDO AL TEXTO, PROPUESTO COMO LECTURA:

COLOCAR LARESPUESTA ENSEGUIDA DE LA PREGUNTA EN SU CUADERNO.

1.  DONDE COMENZÖ LA HISTORIA DEL ALGEBRA: EN EL ANTIGUO EGIPTO Y BABILONIA.
2.  LOS ANTIGUOS BABILONIOS QUE RESOLVIAN: ECUACIONES CUADRATICAS. 
3. QUE MATEMATICOS CONTINUARON CON LA TRADICION DE BABILONIA Y EGIPTO: Los matemáticos alejandrinos Herón y Diofante
4. A  QUE SE LE LLAMO CIENCIA DE REDUCCION Y EQUILIBRIO: Resolución de ecuaciones
5.  QUIEN ESCRIBIO LOS PRIMEROS LIBROS ARABES DE ALGEBRA: Al−Jwrizm;  matemático egipcio Abu Kamil.
6.  Qué matematico, Enunció y demostró las leyes fundamentales e identidades del álgebra y resolvió problemas matemáticos muy complicados:  Abu Kamil
7. La principal fuente de información sobre la civilización y la matemática babilónica de donde procede :  De textos grabados con inscripciones cuneiformes en tablillas de arcilla.de textos grabados con inscripciones cuneiformes en tablillas de arcilla.
8. LOS TEXTOS DONDE SE ESCRIBIAN: En las tablillas de arcilla.
9. QUE SUCEDE CON LAS TABLILLAS MAS ANTIGUAS:
10. ESTAS TABLILLAS QUE HAN PROPORCIONADO:
11. QUE NO CONOCIAN LOS BABILONIOS:
12. LA CIVILIZACION EGIPCIA DEJO EVIDENCIA CON LOS PAPIROS, CUALES SON:
13.  LOS PAPIROS QUE CONTIENEN:
14. QUE CONTIENE EL PAPIRO DEL RHIND:
15. QUE CONTIENE EL PAPIRO DE MOSCU:
16. CUAL FUE EL REPRESENTANTE DE LAS MATEMATICAS EN CHINA, SU TEXTO DE LOS NUEVE LIBROS DE QUE TRATA:
17.  PARA LOS MATEMATICOS CHINOS, CUAL FUE SU MAXIMO DESCUBRIMIENTO:
18. APORTES AL DESARROLLO DEL ALGEBRA DE LOS CHINOS:
19. REPRESENTANTES MATEMATICOS INDUES:
20. CUAL FUE EL DESARROLLO MATEMATICO DE LA CULTURA INDU:
21. LA ESCUELA PITAGORICA QUE INCORPORA:
22. LA ESCUELA PITAGORICA A QUE CIVILIZACION CORRESPONDE:

NOTA: FEBRERO 23 SOCIALIZA GOMEZ HEYDI, LUCUMI DERAK, CASTILLO DAVID, 

QUEDA SOCIALIZADO EL TALLER No. 1

NOTACION ALGEBRAICA

sucesiones numericas y geometricas

Utilizamos este enlace para explicar la clase, y que ellos vayan copiando las parte que nos interesa.

https://edu.gcfglobal.org/es/algebra/   ( CURSO DE PREALGEBRA)

 

VER VIDEOS RELACIONADOS CON ESTE TEMA.

PREALGEBRA  ( INTRODUCCION AL  ALGEBRA)

ACTIVIDAD No. 2   

COPIAR  Y RESOLVER EN SU RESPECTIVO CUADERNO. 

RESOLVER LA SIGUIENTE OPERACION DE ACUERDO AL RESPECTIVO ORDEN:

                                12 – 2  . 5  + 1  =

12  –       10    +  1    =   3   

                              –  15 + 8  .  3   –  4    =   

   – 15   + 24      – 4     =  5

 

 

ACTIVIDAD No. 3

ORDEN DE LAS OPERACIONES:  P, E, M y D, S y R.

ACTIVIDAD No. 4

4 / 2 . 3 + ( 4 + 6 .2 ) +  18 / 3 (3 elevado al cuadrado) –  8

  2    .  3    + (  4  +  12  )    +    18 / 9   –  8

     6       +          16            +      2        –    8  =    16

ACTIVIDAD DE REFUERZO:

3  .  4   –  (  5  –  3 ) –  20  / 2 ( elevado al cuadrado)   –  10   = 

 3.  4         – (  2  )              – 20 /  4     –   10  

     12      – 2               – 5       -10   =  –  7

 

ejercicio de refuerzo

 

 

REGLA DE LOS SIGNOS PARA LA SUMA Y RESTA. TODO PARENTESIS PRECEDIDO DEL SIGNO MENOS, HACE QUE CAMBIE LO QUE ESTA DENTRO DEL PARENTESIS. Y CUANDO EL PARENTESIS ESTE PRECEDIDO DEL SIGNO MAS, ESTE HACE QUE LO QUE ESTA DENTRO DEL PARENTESIS, QUEDE TAL COMO ESTA. 

SOCIALIZAR LA PROXIMA CLASE  02 DE MARZO.

 

ACTIVIDAD No. 5

   4 / 2  .  3 + 16  +  18 / 9  –  8  =

NOTA: SE SOCIALIZA LA PROXIMA CLASE.

ACTIVIDAD No. 6

REPASO DE LAS PRIMERAS 20 BASES AL CUADRADO

BASES NEGATIVAS Y EXPONENTES

      ( – 2 )  ELEVADO AL CUADRADO 

NOTA: LA LEY DE LOS SIGNOS SE APLICA SOLAMENTE, PARA LA MULTIPLICACION Y LA DIVISION.  SIGNOS IGUALES DAN COMO RESULTADO POSITIVO, Y SIGNOS DIFERENTES DAN RESULTADO NEGATIVO.  

( -2 ) (- 2) = 4

      ( -3 )  ELEVADO AL CUADRO

 

   ( -3 ) ( -3)  =  9

      (-3 ) ELEVADO AL CUBO 

    (-3)  (-3)  (-3)   =  27

      ( -2 )  ELEVADO AL CUBO

ACTIVIDAD No. 7

VIDEO RELACIONADO CON LOS EXPONENTES. (VER ENLACE)

 

NOTA: PROXIMA CLASE  MARZO 02 CONTINUAR CON LA ACTIVIDAD No. 8 y  REVISAR EJERCICIOS ANTERIORES.

ACTIVIDAD No. 8

MULTIPLICACION DE POTENCIAS ( VER DESPUES DEL VIDEO)

SOCIALIZAR LOS EJERCICIOS DEL VIDEO RELACIONADOS CON LA POTENCIACION.

NOTA: SOCIALIZAR SOBRE ESTE TEMA.  MULTIPLICACION Y DIVISION DE EXPONENTE DE IGUAL BASES Y POTENCIA DE UNA POTENCIA.

ACTIVIDAD No. 09

REPASAR LAS PRIMERAS 2O BASES CON EXPONENTES AL CUADRADO

NOTA: RESOLVER HASTA LA ACTIVIDAD No. 10

ACTIVIDAD No. 10  ( EXPLICAR LA PROXIMA CLASE) 

EXPRESIONES ALGEBRAICAS ( VER REPASO EN LA PRESENTACION HASTA EL FINAL)  INCLUYENDO LA SIMPLIFICACION DE EXPRESIONES ALGEBRAICAS.

NOTA: CONSULTAR TODO LO RELACIONADO CON LAS EXPRESIONES ALGEBRAICAS.

ENLACE DE REFERENCIA:

https://edu.gcfglobal.org/es/algebra/

NOTA: EXPLICAR HASTA SOLUCION DE ECUACION ALGEBRAICAS.

NOTA:  MARZO 9, SE EXPLICA LOS TEMAS DEL ENLACE HASTA POTENCIA DE UNA POTENCIA.

PROXIMA CLASE:  SIMPLIFICACION DE EXPRESIONES ALGEBRAICAS.

DEBEN ESCRIBIR EN EL CUADERNO HASTA LA PROPIEDAD DISTRIBUTIVA.

ACTIVIDAD No. 10

                           1.            6x  –  15 y  +  21  /   3

 

                           2.          16 x  – 20 x   + 36 x  /  4

ACTIVIDAD No. 11

ESCRIBIR LAS SERIES MATEMATICAS (TABLAS DE MULTIPLICAR DOS VECES DEL 2 AL 9)

TAREA: COPIAR DESDE SIMPLIFICACION DE FRACCIONES, HASTA EL ULTIMO EJEMPLO DE LA PROPIEDAD DISTRIBUTIVA. MARZO 16  DE ACUERDO AL ENLACE,)

MARZO 16, PROXIMA CLASE:

* Sucesiones numéricas y geométricas (regla de formación en forma verbal, simbólica y numérica. Elaboración de tablas).

DESARROLLO DEL  TEMA: SUCESIONES NUMERICAS

1. HISTORIA DE LA SUCESIONES, VER ENLACE:  https://prezi.com/n7agu_dq5l7f/historia-de-las-sucesiones-y-las-series/?frame=01ca34b4063935cc9cabc9160cec150f5565c763

ACTIVIDAD No.  12

1.  QUIENES PLANTEARON POR PRIMERA VEZ LAS SUCESIONES ?   LOS BABILONIOS.
2. QUE PROBLEMA PLANTEARON INICIALMENTE ? CUANTO TIEMPO SE DOBLARIA UNA CANTIDAD DE DINERO, A UN DETERMINADO INTERES COMPUESTO. 
3.  QUE FORMULA APARECE POR PRIMERA VEZ ? LA FORMULA DEL INTERES COMPUESTO. 
4. QUE PAPIRO APARECE POR PRIMERA VEZ ?  EL PAIRO DE AHMES O PAPIRO DEL RHIND
5.  QUIEN LO DESCUBRE  Y EN QUE AÑO ? HENRY RHIND, EN 1858
6. CUANTO MIDE EL PAPIRO ?  6 M DE LARGO Y 33 CM DE ANCHO.
7. QUE REPRESENTA EL PAPIRO ?
8.  COMO ESTA ESCRITO EL PAPIRO ?  EN HIERATICO.
9.  QUE SIGNIFICA EL TERMINO HIERATICO?   PERMITE ESCRIBIR RAPIDO.
10. POR QUIEN FUE ESCRITO ESTE PAPIRO DEL RHIND?  AHMES
11.  QUE SUCEDE EN LA INDIA ?  APARECEN LOS MATEMATICOS YAINAS.
12.  QUE SUCEDE EN GRECIA ? 
13. CONSULTAR SOBRE LA SUCESION DE FIBONACI.
14. NOTA: PROXIMA CLASE SOCIALIZAR EL TALLER No. 12  EL CUAL DEBE ESTAR COMPLETAMENTE TERMINADO.

 

1. 13 DE ABRIL  VIDEO DE SUCESIONES NUMERICAS PARA PRINCIPIANTES.
2. https://www.youtube.com/watch?v=xko_-BkpSSs 

 

1. VIDEO DE INTRODUCCION A LAS SUCESIONES. QUE ES UNA SUCESION,  CON EL PROFESOR ALEX.
2. https://www.youtube.com/watch?v=bI99PoaU6P8

 

ACTIVIDAD No. 13

REPASO Y REFUERZO DE LA POTENCIACION Y LA RADICACION, EXPLICADA EN EL CUADERNO.

SANTIAGO DE CALI,  ABRIL  13- 21

TERMINAR Y SOCIALIZAR LA ACTIVIDAD No. 12   HOY DEBE QUEDAR TERMINADA.

LA ACTIVIDAD No. 13  SOCIALIZAR LOS QUE FALTAN

TAREA: VER VIDEO PARA PRINCIPIANTES VIDEO DE INTRODUCCION A LAS SUCESIONES, REALIZAR UN RESUMEN CORTO CON EJEMPLOS EN EL CUADERNO.

SANTIAGO DE CALI, ABRIL 14 DEL 2021

ACTIVIDADES A SEGUIR:

1. REVISION DEL VIDEO PARA PRINCIPIANTES, QUE HAYAN ESCRITO LOS EJERCICIOS DE ESE VIDEO.
2.     1, 3, 5, 7,  CUAL SIGUE ?
3.     3, 6, 9, 12
4.    6, 11, 16, 21

TAREA:

1.       5, 10, 15, 20… CUAL SIGUE
2.       4, 8, 12,
3.        6,12, 18….
4.       7, 14, 21….
5.        8, 16, 24
6.       9, 18, 27….

……………………………………………………………………………………………………

SANTIAGO DE CALI, JUNIO 22 DEL 2021

SE CIERRA EL PRIMER PERIODO CON EL TEMA DE SUCESIONES, EL CUAL DEBE QUEDAR EN SU RESPECTIVO CUADERNO.

 

---

SEGUNDO PERIODO

ESTANDAR:  Utilizo números reales en sus diferentes representaciones y en diversos contextos.

DESEMPEÑOS: Determina si un número es real y a que
subconjuntos pertenece,
* Reconoce la existencia de los números
irracionales y los ubica en la recta
numérica usando representaciones
geométricas.
*Construye representaciones
geométricas y numéricas de los números
reales (con decimales,
raíces, razones, y otros símbolos) y
realiza
conversiones entre ellas.
* Ubica números reales en la recta
numérica.
* Determina si un número real es mayor,
menor o igual a otro.
* Aplica propiedades para solucionar un
problema que involucra adición y/o
multiplicación en el conjunto de los
números reales.
* Identifica y representa en forma
verbal, simbólica y gráfica intervalos de
números reales.

APRENDIZAJES: Utilizo números reales en sus
diferentes representaciones y en
diversos contextos.

EJES CONCEPTUALES:

Números reales: naturales, enteros,
racionales e irracionales. (Ubicación en la
recta numérica, orden, distancia, valor
absoluto, operaciones con reales para
calcular distancias, perímetros, áreas y
volúmenes, etc.)
* Intervalos en la recta numérica
(representación simbólica, desigualdad,
gráfica, verbal).

ACTIVIDADES PARA  EL SEGUNDO PERIODO

EJE TEMATICO DEL PRIMER PERIODO: ( POR TERMINAR)

Ecuaciones lineales de una variable (coeficientes racionales, operaciones de polinomios, resolución de problemas).

EJES TEMATICOS DEL SEGUNDO PERIODO:

*Plano cartesiano *Sistema de ecuaciones lineales *Conjuntos numéricos (operaciones) *Radicación (operaciones, definición de números complejos) *Teorema de Pitágoras *Números irracionales (concepto y operaciones).

NOTA: CLASE PARA EL DIA 28 DE JULIO   ( REGRESO A LA VIRTUALIDAD)

ACTIVIDAD No. 1   PARA COPIAR EN EL CUADERNO

TEMA: ECUACIONES LINEALES

Una ecuación debe de tener un signo de igual, como en 3 x + 5 = 11. Una ecuación lineal es aquella donde la(s) variable(s) están multiplicadas por números o sumadas a números.

Una ecuación en matemática se define como una igualdad establecida entre dos expresiones, en la cual puede haber una o más incógnitas que deben ser resueltas. … Las ecuaciones pueden tener una o más incógnitas, y también puede darse el caso de que no tengan ninguna solución o de que sea posible más de una solución.

 

NOTA: LAS LETRAS SON VARIABLES, Y LAS CANTIDADES SOLAS ( 2, -3 etc) SE LES LLAMA TERMINOS INDEPENDIENTES. ES NECESARIO UTILIZAR EL CONCEPTO DE LOS NUMEROS ENTEROS Y LA LEY DE LOS SIGNOS.

LA AGRUPACION DE TERMINOS.

LA TRANSPOSICION ES CAMBIAR UN TEMINO DE UN LADO A OTRO, PERO CON SIGNO CONTARIO.

 

EJEMPLO No. 1

 

EJEMPLO No. 2    NOTA:  APLICAMOS LA PROPIEDAD DISTRIBUTIVA,  APLICAMOS LA LEY DE LOS SIGNOS PARA LA MULTIPLICACION Y LA DIVISION.  ( SIGNOS IGUALES, DA POSITIVO, Y SIGNOS DIFERENTES DA NEGATIVO) APLICAMOS TRANSPOSICION DE TERMINOS, LO  QUE SIGNIFICA, CAMBIAR DE UN LADO A OTRO, PERO CON SIGNO DIFERENTE.

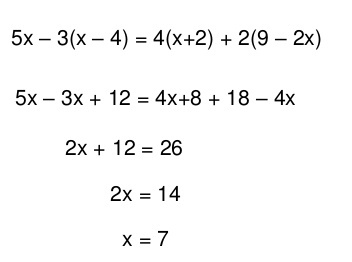
EJEMPLO No. 3

 

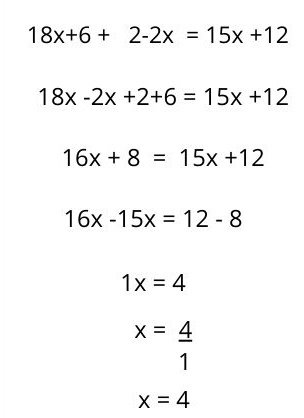
EJEMPLO No. 4

 

 

EJEMPLO No. 5

 

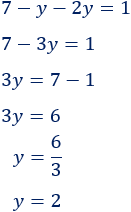
EJEMPLO No. 6

 

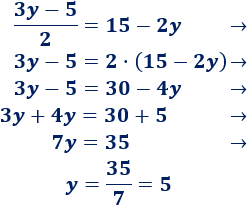
EJEMPLO No. 7

 

EJEMPLO No. 8

 

 

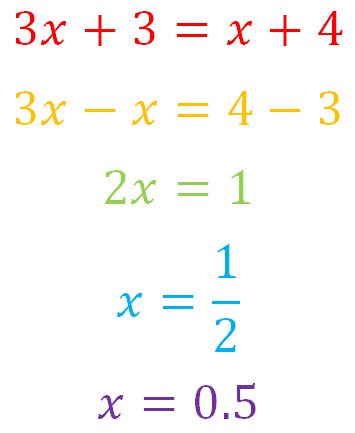
https://www.algebra.jcbmat.com/id1151.htm

ENTRAR POR INDICE TEMATICO Y SE BUSCA  EL EJERCICIO No. 75

      TRABAJAMOS DESDE EL  EJEERCICIO No. 1 HASTA EL   EJERCICIO No. 9

……………………………………………………………………………………………………………………………………………..

SANTIAGO DE CALI, AGOSTO 03 DEL 2021 

CLASE No. 2

ALGEBRA DE  BALDOR

https://guao.org/sites/default/files/biblioteca/%C3%81lgebra%20de%20Baldor.pdf

NOTA: EL LIBRO DE AURELIO BALDOR SERA LA GUIA PARA EL TRABAJO DEL SEGUNDO PERIODO.

SE INICIA DESDE LA PAGINA No. 122

TEMA: ECUACIONES DE PRIMER GRADO

COPIAR LA TEORIA DE LAS PAGINAS 122- 123- 124- 125 –  126

EL TALLER DE ECUACIONES SE ENCUENTRA EN LA PAGINA No. 127

SE COPIAN LOS PRIMEROS 5 EJERCICIOS

SE EXPLICA EL EJERCICIO No. 5  Y SE EVALUA EN CLASE EL No. 1

TAREA: RESOLVER LOS TRES EJERCICIOS QUE FALTAN.

SE EXPLICA EJERCICIO DE LA PAGINA No. 128 

EL CUAL SE DEBE COPIAR EN EL CUADERNO.

…………………………………………………………………………………………………………………………………….

SANTIAGO DE CALI, AGOSTO 4 DEL 2021

CLASE No. 3

1. SE REVISAN LOS  3  EJERCICIOS QUE SE DEJARON LA CLASE ANTERIOR
2. SE EXPLICA EL EJERCICIO No. 2 DE LA PAGINA No. 128  Y EL ESTUDIANTE RESUELVE EL  EJERCICIO No. 1
3. COPIAR EL SIGUIENTE TEXTO Y REALIZAR UNA REFLEXION AL RESPECTO. (SE ENVIA AL GRUPO DE MATEMATICAS.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

SISTEMA DE ECUACIONES LINEALES

Los sistemas de ecuaciones lineales los podemos clasificar según su número de soluciones: Compatible determinado: Tiene una única solución, la representación son dos rectas que se cortan en un punto. Compatible indeterminado: Tiene infinitas soluciones, la representación son dos rectas que coinciden.

En la vida diaria, resolver una ecuación lineal, nos permite estudiar costos, ofertas, demandas, gastos, consumos y otros. Por ejemplo, el consumo y costo de la electricidad se puede medir con una ecuación lineal la cual nos puede ayudar a predecir los pagos que realizaremos o cómo disminuir los gastos por el consumo.

PARA ESTE EJEMPLO APLICAMOS EL METODO DE SUSTITUCION:

 

EL METODO GRAFICO:

EJEMPLO No. 1

DESPEJAMOS A LA VARIABLE Y, EN CADA ECUACION.

X – Y  = -1

– Y  =  -1 -X  LA VARIABLE Y NO PUEDE QUEDAR NEGATIVA,

POR LO TANTO MULTIPLICAMOS POR  – 1 A   AMBOS MIEMBROS

DE LA IGUALDAD.

(- 1)    – Y   = -1  -X     (-1)    QUEDA ENTONCES

Y  =   1  + X

CON ESTA ECUACION, COMENZAMOS A REEMPLAZAR LOS VALORES DE  “X” QUE NOS DAN EN LA TABLA. LUEGO ESE  VALOR SE COLOCA EN  ” Y ”

NOTA: LO MISMO  SUCEDE CON LA SEGUNDA ECUACION.

2X  – Y  =   1

– Y   =   1    -2X

POR LO TANTO MULTIPLICAMOS POR  – 1 A   AMBOS MIEMBROS

DE LA IGUALDAD.

( -1 )    –  Y    =  1    –    2 X     ( – 1 )

Y  =   -1   +   2 X

 

 

 

 

EJEMPLO No. 2

LA PRIMERA PARTE ES DESPEJAR  “Y ” , EN   LAS ECUACIONES.

1.       2X +  Y    =  7        ENTONCES QUEDA:     Y = 7 – 2X

2.        2 X -1   =  Y          ENTONCES QUEDA:     Y = 2 X – 1